Dean Eigenmann

In this post we are gonna discuss an often referenced problem in distributed systems known as “The Byzantine Generals’ Problem”. We will also have a brief look at the Two Generals’ Problem, sometimes referred to as the “Chinese Generals’ Problem”, which I sometimes see confused with the Byzantine Generals’ Problem.

The Byzantine Generals’ Problem is another paper by Leslie Lamport, the author of the paper we looked at in my first post “Time, clocks, and order”. The paper was co-authored by Marshall Pease and Robert Shosta and published in 1982. It can be considered a follow-up of the original “Reaching Agreement in the Presence of Faults” paper.

First there were two

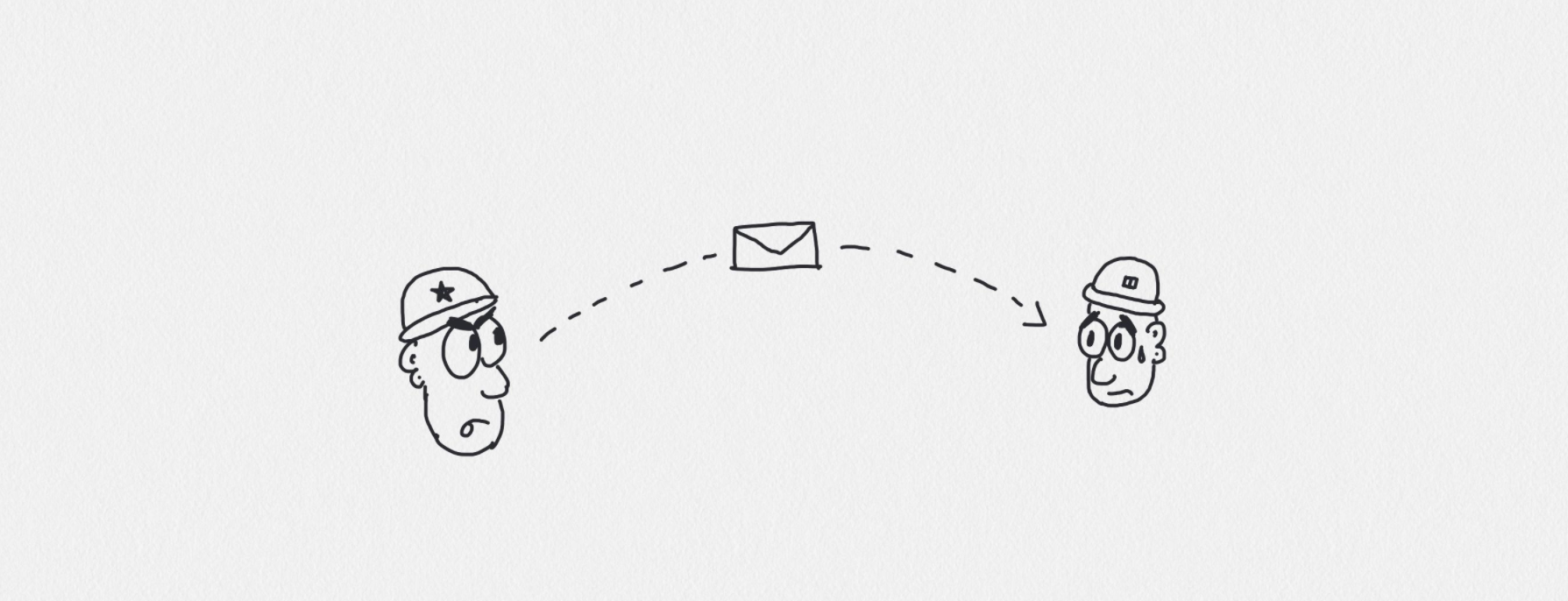
Let’s first look at the two generals’ problem: it’s one of the first widely known distributed consensus problems and concerns itself with reaching consensus on an unreliable link. We’re gonna look at the problem first and show that it’s impossible to truly reach consensus when the link is unreliable.

The setup of the problem is very simple and was first described by Jim Gray in “Operating Systems: An Advanced Guide”. There are two armies on opposite sides of an enemy. They must decide on whether to attack or retreat. If only one of them attacks, they will be slaughtered, meaning they must be in agreement on what to do. In order to coordinate on a strategy, the two generals can only communicate using a carrier pigeon which can get lost.

It is impossible to achieve consensus in the above scenario. Let’s say one of the generals wants to attack, so they send a message to the other general. That message can either be delivered by the pigeon or the pigeon gets lost, meaning the message never gets delivered. The sender has no idea which happened, therefore cannot attack with the certainty that the other will also attack.

You may think to yourself “acknowledgements!”, but those also travel by our pigeon, meaning they could get lost. The sender is thereby yet again uncertain whether that message was received, meaning they cannot be sure whether the other will attack or not. This cycle of uncertainty continues even if we layer acknowledgements. We could send hundreds of acknowledgments, acknowledging acknowledgments that acknowledge acknowledgments and still not be sure.

And then the rest arrived

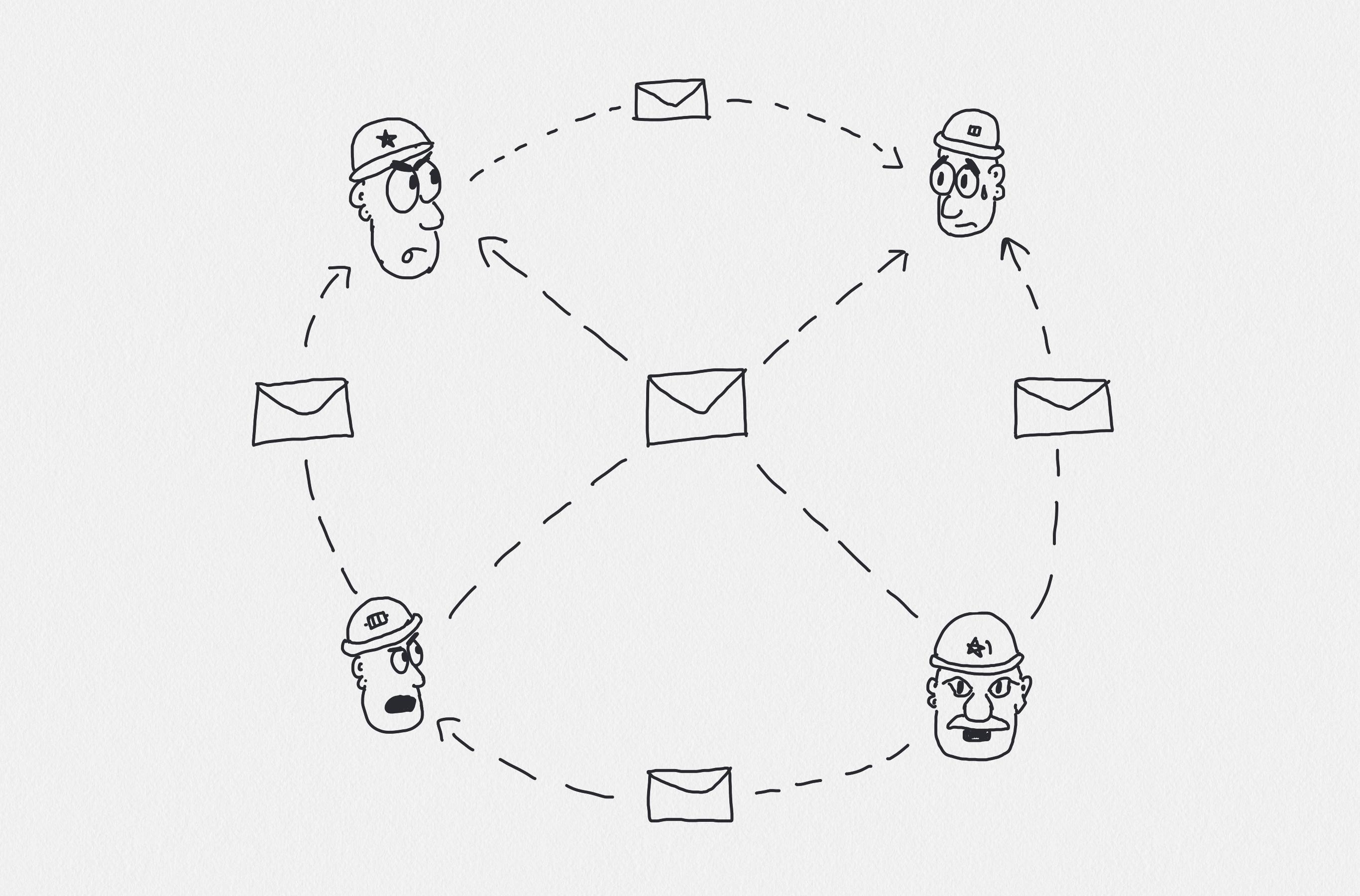
Now with the Byzantine Generals’ Problem, let’s add add more generals, some of whom may be traitors and will attempt to deceive other generals, preventing them from achieving consensus. This problem will show us how we can implement a reliable computer system.

To be able to achieve consensus while these traitors are present, the other generals must have an algorithm that satisfies the following conditions:

1. All loyal generals will decide on the same plan.
2. A small amount of traitors cannot cause the others to adopt a bad plan.

It’s almost impossible for us to be able to objectively say, or formally prove what a bad plan is. Therefore, we simply say a bad plan is one which the majority did not agree to. In a majority vote, the traitors could only affect the vote if the loyal generals were almost equally divided, this means that we couldn’t really call either decision in this scenario a bad plan.

We can satisfy our first condition by ensuring that all generals use the same method for combining all received messages.

You may be thinking that the easiest way to solve this would be for every general to send their opinion by a messenger to every other general. This however does not work, because our first condition would require all generals receive the same messages, but a traitor could send different messages to each of the generals.

So to be able to satisfy our first condition, every general must obtain the same information. This means that we cannot use the message the general sent us directly, since a traitor may send different values to different generals. Additionally, we can say that if a general is loyal, then the message they send must be used by all other loyal generals.

That’s a lot to think about, but we can reduce it down to this:

Any two generals must use the same message for a specific general, whether or not that specific general is loyal.

Knowing this, we can restrict our consideration to the problem of how a single general sends his message to other generals. Therefore, we can simplify the problem even further.

We say that all generals must send their order to all other generals such that:

• IC1 - All loyal generals obey the same order.
• IC2 - If the commander is loyal, then all other generals obey the order.

IC1 follows from IC2 if the general is loyal. We call these conditions interactive consistency conditions.

Oral Messages

So now let’s look at the Byzantine Generals’ Problem when generals can only send oral messages. An oral message is one whose contents are completely under the control of the sender, meaning a traitor can send any possible message.

The Byzantine Generals’ Problem may seem simple, however if we can only send these oral messages, then no solution will work unless more than two-thirds of the generals are loyal. This means that with 3 generals, there is no solution that can work with even a single traitor.

Now it’s time to prove that no solution can work as stated above. Firstly, we allow for two possible decision, either attack or retreat.

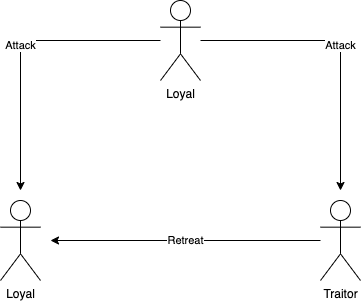
Let’s assume we have 3 generals, one general sends an attack order to both of the others. One of those generals however is a traitor and reports to the other that he received a message saying he should retreat rather than attack. If we were to satisfy IC2, the loyal general should obey the attack order.

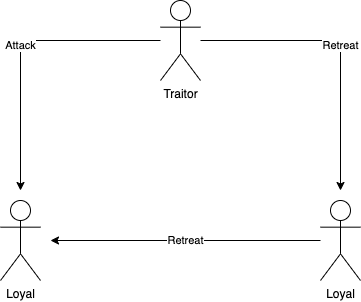
Now let’s consider a second scenario, our general sending messages to the other is now a traitor and sends an attack message to one of the other generals and a retreat message to the other. In both scenarios, our loyal general does not know who the traitor really is and hence to that general both of the scenarios are completely identical.

If our traitor continues to lie, then the loyal general has no way to distinguish the situation and must honour the attack message. Meaning, whenever a general receives an attack from the commander he must obey it. The same thing can be said in the other direction, if a general receives a retreat from a commander he must obey it even if the other general states he received an attack message.

Therefore, in our above scenario one general obeys the attack, while the other obeys the retreat. This violates our condition IC1, which states that all generals must obey the same order, concluding that no solution can work for 3 generals with a single traitor.

Approximate Agreement

You may think this problem is hard due to the requirement to reach exact agreement. However, reaching approximate agreement is just as hard.

Let’s assume this, the generals need to agree on an approximate time of when to attack. To do this, we require the following conditions:

• IC1` - All loyal generals attack within 10 minutes of one another.
• IC2` - If the commander is loyal, then all other attack within 10 minutes of the time given by the commander.

We assume that the messages are sent and processed far in advance, meaning that agreement could be reached in time.

This problem is unsolvable just as the above, unless more than two-thirds of the generals are loyal. We can state this, because if we could solve this problem for a solution with three generals that was able to cope with one traitor then we could construct a three general solution to the Byzantine Generals’ Problem that also worked in the presence of one traitor.

A solution with oral messages

So we have shown that to deal with $m$ traitors, we need $3m + 1$ generals. So let’s now construct an algorithm that works for our $3m + 1$ generals.

Firstly, we make the following assumptions for oral messages:

1. Every message that is sent is delivered correctly.
2. The receiver of a message knows who sent it.
3. The absence of a message can be detected.

The first two assumptions means that a traitor cannot interfere with the communication between two generals. Whereas the third stops a traitor from preventing a decision being made by not sending any messages.

Additionally, we make the assumption that all generals can send messages directly to every other general.

Finally, we need some kind of default. Because traitors may decide not to send a message, in our case we will use retreat as our default.

So let’s define our algorithm $OM(m)$, where a general sends an attack or retreat message to $n - 1$ generals ($n$ being the total number of generals). This will solve Byzantine Generals Problem for $3m + 1$ generals with $m$ traitors.

Firstly, our algorithm defines a function called $majority$, this function either returns the majority of the received orders, or the default value, in our case retreat.

For $OM(0)$ or when we have no traitors, the algorithm works as follows:

1. The general sends his value to every other general.
2. Each general uses the value they receive from the other or uses the retreat if no value was received.

So now let’s look at it for $OM(m), m > 0$, or in other words the scenario where we have more than 0 traitors.

1. The general sends his value to every other general.
2. The other generals then either store the value, or the default value if nothing was received. The other generals then rerun the algorithm with $OM(m - 1)$ sending their stored value to the others.
3. The generals then again store those received values, or the default if none was received. Finally, they run the $majority$ function using all the stored values to get the result.

So now that we see how the algorithm works, let’s look at how it would work for 4 generals with a single traitor.

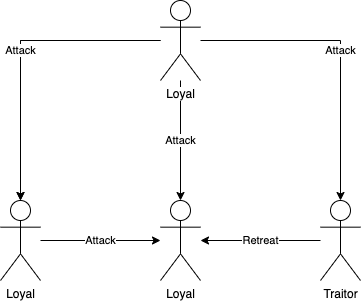
Firstly, a general sends their value to the others. Then one of the loyal generals sends their value to the others, while the traitor sends another value to the other general too. Our loyal general has no received 3 values, they can then run the $majority$ function using these 3 values to get the correct one, this would be the value they received from the loyal generals.

Let’s assume however our first general is malicious. If he sends 3 random values to all the generals, after running the algorithm recursively, every general has 3 random values. This would mean that the majority of those random values is used.

A solution with signed messages

The Byzantine Generals’ Problem is hard to solve because our traitors can lie, however we can remove this ability. One way to do this is by ensuring that the generals send unforgeable signed messages. This means that we add the following assumptions to our previously made assumptions on what an oral message embodies:

1. A loyal general’s signature cannot be forged and any alteration of the contents of his signed message can be detected.
2. Anyone can verify the authenticity of a general’s signature.

We make no assumptions on a traitor general’s signatures, this means that traitors could collude with each other. However, for this solution to hold, we still assume that all generals can talk to one another. With our signature introduced, our previous argument saying we need $3m + 1$ generals to cope no longer holds. We can now construct an algorithm that copes with $m$ traitors for any given number of generals.

In our new algorithm the general sends a signed message to the other generals. Each of which then adds their signature to it and sends it to the others, who in turn add their signatures and send it to the others, and so on. Generals can now know if another is a traitor by simply checking whether several signed messages were received originating from the same general.

In conclusion, the Byzantine Generals’ Problem highlights the difficulty of reaching consensus when nodes can fail in arbitrary ways. The paper goes into further details of how to solve the problem when the generals cannot communicate with all generals, however we’ve omitted that as it would just become too long of a post. I recommend you check out the paper however!

Shoutout to @ricburton for the drawings