Dean Eigenmann

Having decided to start a newsletter on distributed systems to get back into writing, I thought about what a good first subject would be. Maybe AZTEC protocol, a confidential transactions protocol on Ethereum or Paxos, the consensus protocol designed by Leslie Lamport with a reputation of being hard to grasp. Those are all topics I will most likely write about in the future. But, for my first post I decided to go with something more fundamental: the notion of time in a distributed system and the ordering of events.

This post will explain the concepts found in a paper by Leslie Lamport called “Time, clocks, and the ordering of events in a distributed system”. I read this quite a while ago, so it was fun to read it again and summarize the key concepts. For those of you who aren’t familiar with Leslie Lamport, he is known for creating LaTeX, TLA+, Paxos, describing the Byzantine Generals Problem and of course Lamport Clocks which we will be looking at in this post.

Before we begin, let’s define what a distributed system is. We will use Lamport’s definition from the paper directly:

“A system is distributed if the message transmission delay is not negligible compared to the time between events in a single process.”

I like this definition because it makes no comments on anything other than the latency between the sending and receiving of messages.

Now we are ready to get started.

Order

Sometimes we need to order events. This is really simple to do locally; all one has to do is assign a timestamp to every event when it occurred and we are done. We now have a total order of all our events which means that all events can be placed into a specific order.

Yet, the problem gets a lot harder in the context of a distributed system.

Why is this the case?

It all comes down to one very simple property of distributed systems: messages sent between nodes may arrive zero, one, or multiple times at any point in the future after they are sent. This property makes it impossible to agree on time between multiple nodes. One node could send another node a message stating that the current time is 12:00:00, but the recipient will not know how long the message took to arrive, and thus cannot confirm whether the time is still 12:00:00 upon arrival. Nodes can send these messages back and forth all day and never actually be sure if they are synchronized. If we can’t agree on time, we also can’t fully agree on the order of events.

So what can we do? Well, in a distributed system, multiple nodes communicate through messages. When a node receives a message, it acknowledges it and then executes its next event. This sequence of events indicates causality.

We know for a fact that a message must be sent before it can be received. So we can be sure that sending a message happened before it was received, giving a “happened before” relationship in the context of these two events. This relationship can therefore be recognized without needing the notion of time in a system: we can say that event A happened before event B, if A causally affected B.

Causal order provides us with a partial order of events in our system, meaning we can be sure that dependent events are ordered. There is, however, a limitation of partial ordering: we may not know the exact order of every event in the system because they may not be causally related. This is because it is possible to have concurrent events happening across the system of which not all nodes are aware.

Clocks

Now once we’ve achieved this partial ordering, let’s add clocks to our system. This will allow us later to totally order all the events in our system.

So we already discussed why we can’t use time in a distributed system, meaning physical clocks are out of the question. So what we need to use are logical clocks. A logical clock is essentially a function with the ability to assign a number to an event. This number represents the time at which an event occurred (we will refer to this number as time from now on), without having any relation to the actual physical time.

Every node in our distributed system now has a clock. This clock ticks between every event executed, but the clock tick itself is not considered an event within our system. So for every event occurring on a node in the system, a number is assigned to that event. With this assumption we can satisfy the following clock condition:

But what does this actually mean?

Let’s break it down: we used the arrow $\rightarrow$ to denote the “happened before” relationship and $C$ is our clock function. With that, we can translate the above condition as follows: for every event \(a\),\(b\), if \(a\) happened before \(b\), then the time of \(a\) is smaller than that of \(b\).

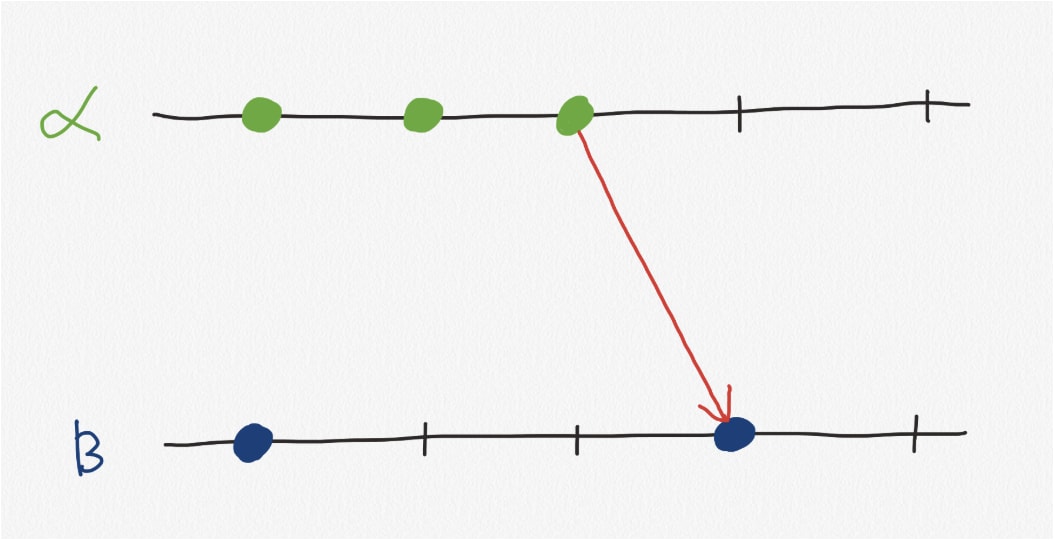
The converse does not hold, just because the time of an event is smaller than another, does not mean that the event happened before, they could be concurrent. In the above image, we can see events on Node α happened at time 1 and time 2. Node β had an event at its own time 1. Therefore, events on α during time 1 and 2 are concurrent to the event on β at time 1 because they were not causally related.

This clock condition is satisfied by the following conditions:

• If \(a\) and \(b\) are events on a single node, and \(a\) happened before \(b\), then the time of \(a\) should be smaller than that of \(b\).
• If \(a\) is a node sending a message, and \(b\) is the receipt of that message on another node then the time of \(a\) should still be smaller than that of \(b\).

There is a simple solution to satisfying the above conditions: a node needs to tick its clock between events, and it must advance its clock to be later than the time contained in any received messages from other nodes if it is not. \(b\) can then occur after advancing the clock.

Now comes the fun part - we can use these clocks that satisfy our clock condition to establish a total order of our entire distributed system! We simply order the events by the time given by their clocks, and for any ties, we break them using an arbitrary order.

In practice

Finally, let’s define a state machine that shows the utility of these logical clocks. So, we have a distributed system with a shared resource that multiple nodes want to access, but only one can access it at a time. We want our state machine to satisfy the following conditions:

1. A node that has access to a resource must release it before another can access it.
2. Requests for the resource must be granted in the order of which they are made.
3. If every node which is granted access eventually releases it, then every request is eventually granted.

We could introduce a central coordinator, but condition 2 would then not be satisfied if an earlier request would only arrive after another due to message latency and we also want to have a decentralized solution. So, we need to solve this somehow with clocks!

Lamport provides us with a solution that is decentralized and satisfies all of our conditions. Firstly, we require all of our nodes to store a queue of request operations. Additionally, for simplicity we make a few assumptions:

1. All messages are received in the order they are sent.
2. All messages are eventually received.
3. We assume that every node can directly send a message to all other nodes in the system.

These assumptions can be avoided by introducing more complex protocols along with the algorithm.

Now that we’ve gotten that out of the way, we can define our algorithm which satisfies our 3 conditions and displays the utility of clocks in practice:

1. If a node wants to request a resource, it creates a request with the current time, adds it to its queue and sends it to every other node.
2. All other nodes put this request into their queue and send back a response.
3. To release a resource, a node sends a release message with the current time and removes the placed request from its queue.
4. When a node receives a release message, it clears the associated request from its own queue.
5. A node is free to access the resource when it has its own request in its queue which is ordered before any other using a total order of the time, and it has received messages from all other nodes later than that time.

The above algorithm is completely decentralized, being independently executed by each node in the system. It makes use of the clock to totally order requests allowing for access coordination of a resource.

That’s it! Now you know how to order events in a distributed system using these logical clocks and how to apply this to an actual problem. Any feedback is appreciated in case I could’ve explained something better!

I will probably be sending out this newsletter once a month.

If you want to see what I read and summarized for this post, check out the corresponding issue on github. Shoutout to @ricburton for the drawings & @renelubov for the help!